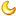/*---------------------------------------------------------------------------
File name: bccn_QHashOverflow.cpp
Author: HJin
6/13/2007 19:21:03
*/
#include <iostream>
#include <cmath>
using namespace std;
/**
This project implements the hash function introduced on
P. 231 of Thoma H. Cormen's seminal book, Introduction
to Algorithms, 2nd ed, MIT press.
The hash function is
h(k) = floor( m * ( k*A mod 1 ) ),
where A = ( sqrt(5) - 1 ) / 2 =0.618... . However, we are not
working with floating-point numbers here. k*A mod 1 is
understood as taking the fractional part of a
floating-point number, say
1.235 mod 1
is 0.235.
Let
w = 32 --- the word length of a 32-bit OS
s = 2654435769, ( s / ( 2^w ) = A )
m = 2^p with p = 14,
k --- the input integer
Then
h(k) = ( (k*s) mod (2^w) )/ (2^w) * 2^p,
or
h(k) = (k*s) shiftting right w-p times.
To reach the formula above, you need to do some math.
Following this idea, I implemented h(k) as below.
However, I cannot overcome the overflow problem at k*s:
s is around 0.618 * (2^w), which makes k*s overflow easily.
Remember that 2^w overflows all integral types.
One idea I thought about is to transform multiplications
into addtions, so that
3*s mod 2^w = ( s mod 2^w ) + ( s mod 2^w ) + ( s mod 2^w ).
Then we fight the overlfow problem existing in the sum, which
is doable. Obviously, this needs O(k) time complexity.
And I don't think it is a good way.
If you have any idea about getting rid of this overflow problem,
please help!
Sample output:
67
1344
11470
5211
15337
9079
2821
12947
6689
431
10556
4298
Press any key to continue . . .
*/
int HashMult(int k, int p=14, int w=32);
int main(int argc, char** argv)
{
int m = 1000;
int k=123456;
cout<<HashMult(k)<<"\t"<<endl;
for(int i=60; i<=70; ++i)
{
cout<<HashMult(i)<<endl;
}
return 0;
}
int HashMult(int k, int p, int w)
{
//// step-by-step construction
//unsigned long s = 2654435769;
//unsigned long r0 = (k*2654435769) & (~0);
//return (r0>>(w-p));
// this also needs some thinking
// MAX is defined to be ~0 = 2^(32)-1
// n mod 2^32 == n & MAX
return ( ( unsigned long(k*2654435769) & (~0) ) >> (w-p) );
}