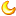算法求助:1231231234 --> 11353 (加加号或者乘号)
Problem statment:You are given a squence of numbers. Put + and * at appropriate places so that the math expression equals the target number. For example,
1231231234 --> 11353
12*3+1+23*123*4 = 11353 // my algorithm shows this example has a unique soln
and two more examples:
"3456237490", 1185 -> "3*4*56+2+3*7+490" // my algorithm shows this example has 3 solns
"3456237490", 9191 -> "no solution"
第三次被问到同一题目了,在面试的时候。我有一个笨的办法:search over all 3^(n-1) possible combinations, where n is the length of the sequence, and use an expression stack to evalute。Obviously, my algorithm is O(3^n), or I have exponential time complexity.
We have around 3^(n-1)choices since we can put +, *, or nothing between two digits:
1+2
1*2
12
The question is: can we have an algorithm of polynomial complexity in time?
First I thought this can be done by using some dynamic programming or greedy algorithms. But I cannot show the optimal substructure or the greedy choice property. (These concepts come from Cormen's Introduction to Algorihtms, MIT press, 2nd ed.)
Do you have any idea?
[此贴子已经被作者于2007-6-9 21:27:56编辑过]