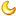帮忙看看这题目哪错了?
Problem E:Rotten RopesTime Limit:1000MS Memory Limit:65536K
Total Submit:123 Accepted:83
Description
Suppose we have n ropes of equal length and we want to use them to lift some heavy object. A tear-off weight t is associated to each rope, that is, if we try to lift an object, heavier than t with that rope, it will tear off. But we can fasten a number of ropes to the heavy object (in parallel), and lift it with all the fastened ropes. When using k ropes to lift a heavy object with weight w, we assume that each of the k ropes, regardless of its tear-off weight, is responsible for lifting a weight of w/k. However, if w/k > t for some rope with tear-off weight of t, that rope will tear off. For example, three ropes with tear-off weights of 1, 10, and 15, when all three are fastened to an object, can not lift an object with weight more than 3, unless the weaker one tears-off. But the second rope, may lift by itself, an object with weight at most 10. Given the tear-off weights of n ropes, your task is to find the weight of the heaviest object that can be lifted by fastening a subset of the given ropes without any of them tearing off.
Input
The first line of the input contains a single integer t (1 <= t <= 10), the number of test cases, followed by the input data for each test case. The first line of each test case contains a single integer n (1 <= n <= 1000) which is the number of ropes. Following the first line, there is a single line containing n integers between 1 and 10000 which are the tear-off weights of the ropes, separated by blank characters.
Output
Each line of the output should contain a single number, which is the largest weight that can be lifted in the corresponding test case without tearing off any rope chosen
Sample Input
2
3
10 1 15
2
10 15
Sample Output
20
20
#include<stdio.h>
main()
{
int f,t,n,num[1005],i,j,k,max;
while(scanf("%d",&t)!=EOF)
{
for(i=1;i<=t;i++)
{
scanf("%d",&n);
for(j=0;j<n;j++)
{
scanf("%d",&num[j]);
}
for(j=1;j<=n-1;j++)
{
for(k=0;k<n-j;k++)
{
if(num[k]>num[k+1])
{
f=num[k];
num[k]=num[k+1];
num[k+1]=f;
}
}
}
max=num[0]*n;
for(j=0;j<n;j++)
{
if(num[j]*(n-j)>max)
max=num[j]*(n-j);
}
printf("%d\n",max);
}
}
}